chu vi là gì và cách tính chu vi là kiến thức cơ bản và quan trọng mà các em học sinh phải nắm được trong quá trình học tập môn Toán. đây cũng là kiến thức rất hay, có công thức tính chu vi từng dạng hình học.
1. Định nghĩa của chu vi là gì?
chu vi là độ dài đo được của một đường kín bao quanh một mặt phẳng hai chiều hoặc chúng ta có thể hiểu chu vi là độ dài của chu vi bao quanh diện tích của một hình. như vậy ta có chu vi hình vuông, chu vi hình chữ nhật, chu vi hình tròn … với các cách tính tương ứng khác nhau.
bây giờ bạn đang xem: chu vi của một biểu tượng là bao nhiêu
2. Chu vi và cách tính chu vi của các hình trong toán học
Trong toán học, có rất nhiều dạng hình khác nhau, chẳng hạn như hình tròn, hình chữ nhật, hình vuông, hình tam giác, hình thang … trong đó, tất cả các hình dạng này đều có chu vi và công thức mà học sinh cần biết. Sau đây là nội dung chi tiết về định nghĩa chu vi và cách tính chu vi hình trong toán học.
2.1. chu vi và cách tính chu vi hình tròn
Chu vi của một hình tròn là độ dài của cạnh của nó. một người sẽ tính chu vi hình tròn theo công thức riêng của mình. Cụ thể, công thức tính chu vi của một hình tròn là lấy pi (lấy nó là 3,14) nhân với đường kính của hình tròn đó, hoặc pi nhân với 2 lần bán kính của hình tròn, vì đường kính bằng bán kính nhân với 2.
Do đó, chúng ta có công thức tính chu vi của một hình tròn:
p = d x pi hoặc p = r x 2 x pi
ở đâu:
+ p là ký hiệu cho chu vi của hình tròn
+ d là đường kính của hình tròn
+ r là bán kính của hình tròn.
+ pi xấp xỉ bằng 3,14. pi được định nghĩa là tỷ số của chu vi hình tròn.
ví dụ: tính chu vi của một bánh xe có đường kính 0,75 m.
Trả lời: Đây là một bài toán đơn giản, có một phép tính bạn chỉ cần áp dụng công thức trên và thay số vào phép tính. từ tiêu đề cho đường kính của hình tròn, bạn biết số pi.
khi đó chu vi của bánh xe tròn đó là: p = d.pi = 0,75 x 3,14 = 2355 (m)
như vậy, chu vi của hình tròn là 2355 (m)
2.2. chu vi và cách tính chu vi hình chữ nhật
Tương tự như định nghĩa chung về chu vi, chu vi hình chữ nhật là độ dài của đoạn thẳng bao quanh một mặt phẳng hình chữ nhật. còn hình chữ nhật có bốn góc vuông nên cũng là hình bình hành và hình thang cân phải có đầy đủ các tính chất của hình cân và hình bình hành.
do đó, tổng chiều dài cộng với hai lần chiều rộng là chu vi của hình chữ nhật. chúng ta có công thức sau để tính chu vi hình chữ nhật:
p = (a + b) x 2
ở đâu:
+ a là ký hiệu cho chiều dài của hình chữ nhật
+ b là ký hiệu cho chiều rộng của hình chữ nhật
+ p là chu vi của hình chữ nhật
Ví dụ: tìm chu vi của một cái bánh hình chữ nhật khi độ dài các cạnh tương ứng là 6 cm và 3 cm.
đáp án: đầu bài cho biết chiều dài chiều rộng và chiều dài của chiếc bánh hình chữ nhật. vì vậy, chúng ta chỉ cần áp dụng công thức tính chu vi trên rồi đổi số, đặt tính là được kết quả.
chúng ta có công thức tính chu vi hình chữ nhật: p = (a + b) x 2 = (6 + 3) x 2 = 9 x 2 = 18 (cm)
vậy chu vi của chiếc bánh hình chữ nhật là 18 cm.
2.3. chu vi và cách tính chu vi hình vuông
Chu vi hình vuông là độ dài của đoạn thẳng bao quanh một hình hoặc hình vuông hai chiều. Hình vuông là hình có 4 cạnh bằng nhau và 4 góc vuông 90 độ. do đó, việc tính chu vi hình vuông khá đơn giản, theo công thức sau:
p = a x 4
ở đâu:
+ a là bất kỳ cạnh nào của hình vuông
+ p là chu vi của hình vuông.
xem thêm: bệnh tăng nhãn áp là gì
Nói ngắn gọn, chu vi hình vuông là tổng độ dài 4 cạnh của nó hoặc độ dài một cạnh nhân với 4.
ví dụ: cung cấp cho chiều dài của cạnh hình vuông của bảng là 6 cm. Tính chu vi hình vuông của tấm ván đó.
đáp án: bài toán nói về một cạnh góc vuông, vì vậy chúng ta có thể áp dụng công thức tính bình phương và thay thế số phép tính. chúng ta có công thức p = a x 4 = 6 x 4 = 24 (cm)
vậy chu vi của cái bàn đó là 24 cm.
2.4. chu vi và cách tính chu vi hình tam giác
tam giác là một hình gồm 3 cạnh như tên gọi của nó. ta có tam giác thường, tam giác vuông có góc vuông 90o và tam giác đều có 3 cạnh bằng nhau hoặc tam giác cân, tam giác tù, tam giác nhọn và tam giác vuông cân. Tuy là các tam giác khác nhau nhưng chu vi của tam giác vẫn là tổng của 3 cạnh cộng lại với nhau. tùy thuộc vào tính chất của từng hình mà bạn sẽ có công thức tính khác nhau một chút.
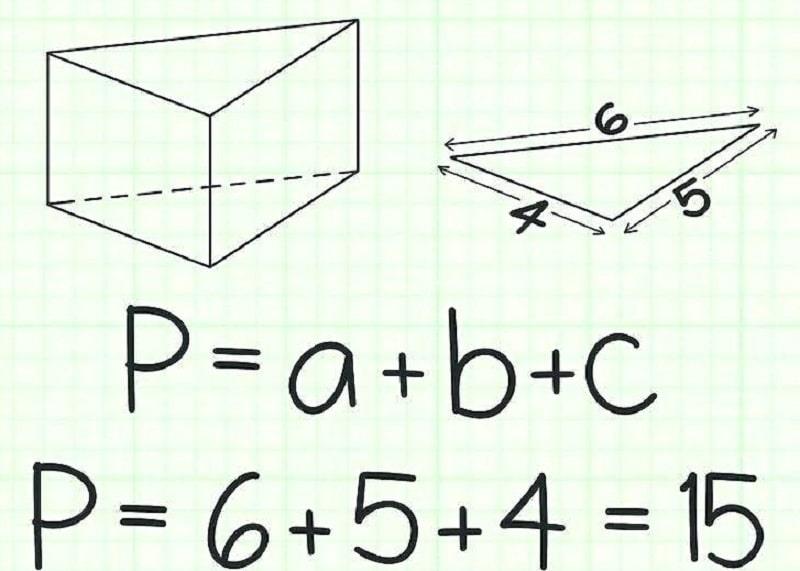
a. Cách tính chu vi của hình tam giác thường
tam giác thường là một tam giác có các cạnh và góc khác nhau. hình tam giác thường có các cạnh khác nhau có chung cách tính chu vi là tổng 3 cạnh cộng lại với nhau. Chu vi hình tam giác thường bằng tổng ba cạnh. công thức tính chu vi hình tam giác thường là p = a + b + c. trong đó: a, b, c lần lượt là 3 cạnh của tam giác.
ví dụ: tìm chu vi của một tam giác bình thường abc khi độ dài các cạnh tương ứng là 2,3,4 cm.
Trả lời: Vì bài toán cho độ dài 3 cạnh của tam giác nên ta áp dụng công thức p = a + b + c = 2 + 3 + 4 = 9 (cm). vậy chu vi của tam giác đã cho là 9 cm.
b. tính chu vi tam giác vuông
Một vết lồi có 3 cạnh và một góc vuông là một tam giác vuông. cách tính chu vi tam giác vuông theo công thức sau:
p = a + b + h
ở đâu:
+ a và b là hai cạnh của tam giác vuông đó.
+ h là chiều cao của tam giác, nối nó từ trên xuống dưới.
c. công thức tính chu vi của tam giác cân
Chu vi của tam giác cân được tính bằng công thức: p = a + b + c
Vì là hình vuông cân nên nó sẽ được tính là 2a + c hoặc 2b + c.
d. công thức tính chu vi của tam giác đều
Tam giác đều là hình có 3 cạnh bằng nhau, vì vậy công thức tính chu vi sẽ là p = a x 3 = b x 3 = c x 3 .
vậy, chu vi của hình tam giác ngắn gọn là tổng 3 cạnh của hình đó cộng lại. Tuy mỗi tam giác đều có những đặc điểm và tính chất riêng nhưng tổng chu vi sẽ có những cách tính tổng tương ứng.
2.5. tính chu vi hình bình hành
Một tứ giác có 2 cặp cạnh đối song song bằng nhau là hình bình hành. là một hình thang đặc biệt có các góc đối diện bằng nhau. do đó, chu vi của một hình bình hành bằng tổng của bất kỳ cặp cạnh kề nào nhân với 2. hoặc chu vi của một hình bình hành là tổng độ dài của bốn cạnh của hình đó.
Chúng ta có công thức sau để tính chu vi: c = 2 (a + b). ở đâu:
+ a và b: là hai cạnh bất kỳ của hình bình hành.
+ c là kí hiệu của chu vi hình bình hành.
ví dụ: tìm chu vi của một miếng bánh hình bình hành khi độ dài các cạnh a = 4 cm, b = 8 cm.
đáp án: đề bài cho 2 cạnh kề của hình bình hành nên ta áp dụng công thức tính chu vi hình bình hành c = 2 (a + b) = 2 (4 x 8) = 2 x 12 = 24 (cm)
vậy chu vi của mảnh hình bình hành là 24 cm.
2.6. chu vi và cách tính chu vi hình thang
Hình thang là tứ giác lồi có 2 cạnh đáy song song và các cạnh bên còn lại. trong đó, có một hình thang vuông có góc vuông 90o và hình thang cân có 2 góc kề cùng đáy.
Do đó, tổng độ dài hai đáy và hai cạnh bên là chu vi của hình thang. nghĩa là, chu vi của hình thang sẽ bằng tổng của tất cả các cạnh cộng lại.
Công thức tính chu vi hình thang như sau:
p = a + b + c + d
ở đâu:
+ p biểu thị chu vi hình thang
+ a, b, c, d là các cạnh của hình thoi.
Ví dụ: tính chu vi hình thang biết rằng đáy lớn dài 10 cm, đáy nhỏ 8 cm và 2 cạnh bên lần lượt là 6 cm và 9 cm.
đáp án: bài toán cho biết độ dài 2 đáy và 2 cạnh bên nên phải áp dụng công thức tính chu vi hình thang: p = a + b + c + d = 10 + 8 + 6 + 9 = 33 (cm)
vậy chu vi của hình thang đó là 33 cm.
xem thêm: người quản lý bán hàng là gì – người quản lý bán hàng giá bao nhiêu
lưu ý: tìm chu vi của hình thang thường hoặc hình thang cân, hình thang vuông bằng nhau, bằng tổng 2 đáy và 2 cạnh cộng lại.
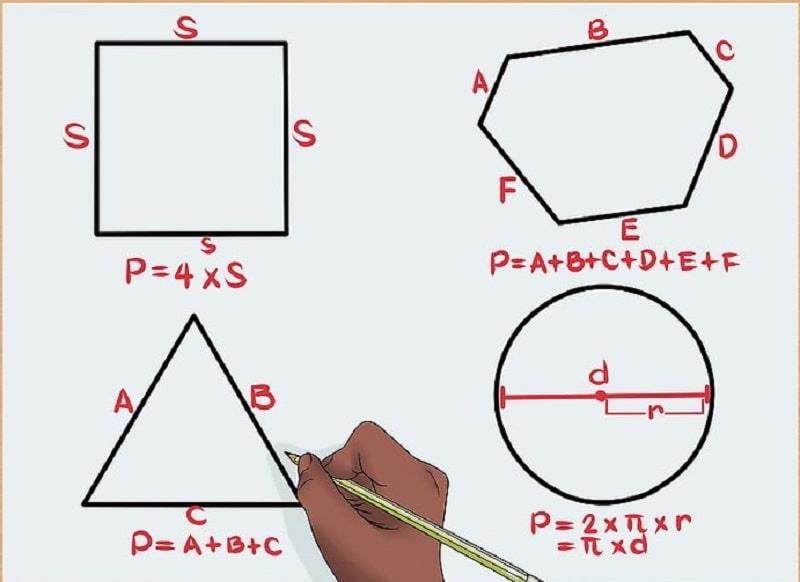
Tóm lại, chu vi của các hình học trong toán sẽ là tổng của các cạnh cộng lại với nhau tương ứng. Nếu là hình tam giác sẽ là tổng của 3 cạnh cộng lại, nếu là hình chữ nhật, hình vuông sẽ là tổng của 4 cạnh cộng lại… Tuy nhiên, mỗi hình sẽ có những tính chất khác nhau mà chu vi cũng theo đó mà có các công thức tương ứng mà bạn cần ghi nhớ. Nhưng nhìn chung, bạn chỉ cần hiểu rằng chu vi chính là tổng của độ dài của đường xung quanh hình mặt phẳng đó để dễ dàng nắm kiến thức hơn. Thêm vào đó, mỗi hình sẽ có các tính chất đặc biệt của nó phân biệt với các hình khác mà bạn cần nắm được sẽ dễ học chu vi của hình hơn cả, dễ tính chu vi hơn.
Tóm lại, chu vi là gì và cách tính chu vi các dạng hình học trong toán học trước đây là những kiến thức quan trọng và được áp dụng rộng rãi trong chương trình học mà các em học sinh nên ghi nhớ.



