Biểu thức toán học là các câu lệnh toán học bao gồm ít nhất hai thuật ngữ chứa số hoặc biến hoặc cả hai, được nối với nhau bằng toán tử. Các toán tử toán học có thể là phép cộng, phép trừ, phép nhân hoặc phép chia. Ví dụ: x + y là một biểu thức trong đó x và y là các số hạng với một toán tử cộng giữa chúng. Trong toán học, có hai loại biểu thức, biểu thức số – chỉ chứa số và biểu thức đại số – chứa số và biến.
Trong bài viết này, chúng ta sẽ thảo luận về khái niệm biểu thức trong toán học và các loại khác nhau của chúng. Chúng ta cũng sẽ hiểu sự khác biệt giữa biểu thức và phương trình ở dạng bảng và xem xét các loại biểu thức khác nhau với sự trợ giúp của các ví dụ để hiểu rõ hơn.
Một biểu thức toán học là một câu chứa ít nhất hai số/biến và ít nhất một phép toán. Hãy hiểu làm thế nào để viết biểu thức. Một số là 6 hơn một nửa số kia, đó là x. Mệnh đề này được viết dưới dạng x/2 + 6 trong các biểu thức toán học. Các biểu thức toán học được sử dụng để giải các câu đố phức tạp.
Định nghĩa biểu thức toán học
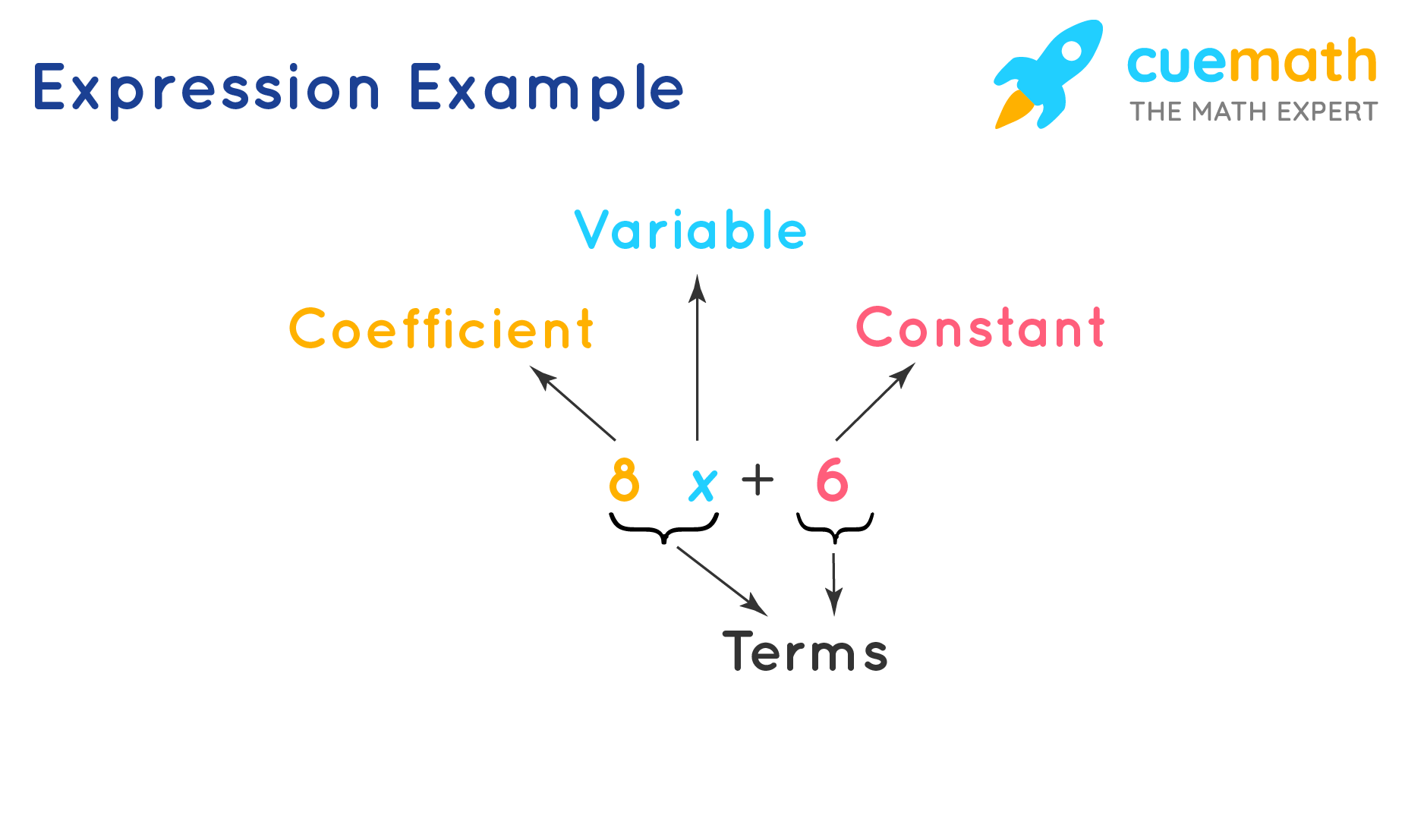
Biểu thức là tổ hợp các thuật ngữ được kết hợp bằng cách sử dụng các phép toán như phép trừ, phép cộng, phép nhân và phép chia. Các thuật ngữ liên quan đến các biểu thức toán học là:
- Hằng số: Hằng số là một giá trị cố định.
- Biến: Biến là một ký hiệu không có giá trị cố định.
- Số hạng: Một số hạng có thể là một hằng số, một biến đơn lẻ hoặc là sự kết hợp của phép nhân hoặc chia các biến và hằng số.
- Hệ số: Hệ số là một số được nhân với một biến trong một biểu thức.
- Biểu thức có 3 phần: hằng, biến và số hạng.
- Có 3 loại biểu thức: số học/số, phân số và đại số.
- Đa thức là một biểu thức biến.
- Phép trừ các biểu thức đại số
- Thêm biểu thức đại số
- Biểu thức hữu tỉ đơn giản hóa
Các biểu thức trong ví dụ toán học
Một biểu thức có vô số trường hợp. Ví dụ: 2y-9, 3a×2, -7+6÷3, v.v. Hãy cũng xem xét một ví dụ thực tế trong cuộc sống. Sarah nói với anh trai Daniel rằng cô ấy hơn gấp đôi tuổi của anh ấy lúc 3 tuổi. Nếu tuổi của anh ấy là x năm, cô ấy yêu cầu anh ấy tính tuổi của cô ấy. Hãy giúp anh ấy viết một biểu thức. Hai lần tuổi của Daniel có thể được viết là 2x. Bây giờ tuổi của Sarah gấp 2 lần 3 tuổi. Do đó, tuổi của sarah sẽ được viết là 2x+3.
Các biểu thức toán học được chia thành ba loại cơ bản. Theo các thuật ngữ chúng có, chúng có thể được chia thành các biểu thức số học/số, biểu thức phân số và biểu thức đại số. Hãy để chúng tôi hiểu thêm về chúng với sự trợ giúp của bảng dưới đây:
Các biểu thức đại số giờ đây được chia thành đơn thức, nhị thức, tam thức, v.v. Chúng còn được gọi là đa thức. Hãy xem các loại biểu thức đại số trong bảng sau:
Trong toán học, biểu thức và phương trình là hai khái niệm khác nhau. Hãy cố gắng hiểu sự khác biệt giữa hai. Biểu thức có thể là số, biến hoặc tổ hợp các số và biến được kết nối bởi các toán tử (tức là cộng, trừ, nhân và chia). Mặt khác, một phương trình là một mối quan hệ bình đẳng giữa hai biểu thức. Hãy xem bảng bên dưới để hiểu rõ hơn:
Phương trình là sự kết hợp của hai biểu thức có dấu “bằng” (=) ở giữa.
Xem thêm một vài ví dụ về biểu thức và phương trình qua hình sau:

Các biểu thức có thể được đơn giản hóa để tạo thành câu trả lời. Ví dụ: 3+6-2 là một biểu thức rút gọn thành 7. Có hai cách khác nhau để đơn giản hóa các biểu thức số học và đại số. Chúng tôi sử dụng quy tắc bodmas (quy tắc pemdas) để đơn giản hóa chúng. Trong trường hợp các biểu thức đại số, các số hạng tương tự có thể được cộng hoặc trừ để đơn giản hóa. Các thuật ngữ tương tự là những thuật ngữ nâng cùng một biến lên cùng một công suất. Do đó, chúng ta có thể dễ dàng cộng hoặc trừ hai hoặc nhiều số hạng giống nhau bằng cách cộng các hệ số của chúng. Ví dụ: kết quả của 2x+5x là 7x và 7ab-b là một biểu thức chứa hai số hạng riêng biệt không thể cộng được.
Đối với các biểu thức có nhiều thuật ngữ và toán tử, chúng tôi áp dụng quy tắc pemdas (quy tắc bodmas). Ví dụ, hãy rút gọn 23 – 6 + 7 × 3. Ở đây, vì không có dấu ngoặc đơn và không có số mũ, trước tiên chúng ta sẽ tính 7 × 3, tức là 21. Bây giờ, biểu thức là 23-6+21. Bây giờ, có hai toán tử, cộng và trừ. Vì cả hai đều là các phép toán theo cùng một thứ tự, nên phép trừ bắt đầu từ bên trái trước, vì vậy chúng ta sẽ trừ 6 từ 23, tức là 17. Bây giờ biểu thức của chúng ta trở thành 17+21, kết quả là 38, là giá trị đơn giản hóa của biểu thức 23 – 6 + 7 × 3.
Lưu ý quan trọng về biểu thức toán học:
Bài viết liên quan
%3Cul%3E+%3Cli%3E%E4%BB%A3%E6%95%B0%E8%A1%A8%E8%BE%BE%E5%BC%8F%E7%9A%84%E5%88%92%E5%88%86%3C%2Fli%3E



