1. Nó được sử dụng khi nào?
Hồi quy hậu cần (thường được gọi đơn giản là hồi quy logistic nhị thức) được sử dụng để dự đoán xác suất của một quan sát rơi vào một trong các loại biến phụ thuộc, liên tục hoặc phân loại, dựa trên một hoặc nhiều biến độc lập có thể có. Mặt khác, nếu biến phụ thuộc của bạn là số đếm, thì phương pháp thống kê bạn nên xem xét là hồi quy Poisson. Ngoài ra, nếu bạn có nhiều hơn hai biến phụ thuộc, bạn nên sử dụng hồi quy logistic đa thức.
Ví dụ: bạn có thể sử dụng hồi quy logistic nhị thức để xem liệu điểm kiểm tra có thể được dự đoán dựa trên thời gian xem xét và sự lo lắng của bài kiểm tra hay không (tức là, biến phụ thuộc là “điểm kiểm tra”, được đo trên thang phân đôi – “đạt” hoặc ” fail “- bạn có hai biến độc lập:” thời gian ôn tập “và” lo lắng khi thi “).
2. Mô hình hồi quy logistic
Mô hình hồi quy hậu cần được sử dụng để dự đoán các biến phân loại từ một hoặc nhiều biến độc lập liên tục hoặc phân loại. Biến phụ thuộc có thể là nhị phân, thứ tự hoặc đa danh mục.
Biến độc lập có thể là khoảng / tỷ lệ, phân đôi, rời rạc hoặc hỗn hợp của những biến này.
Phương trình hồi quy logistic (nếu biến phụ thuộc là nhị thức) là:

trong đó p là xác suất quan sát trường hợp i với giá trị = 1 trong biến kết quả y; e là hằng số toán học Euler với giá trị gần bằng 2,71828; và hệ số hồi quy β tương ứng với biến quan sát.
Chúng tôi thường sử dụng mô hình hồi quy để ước tính ảnh hưởng của biến x đến tỷ lệ cược (y = 1).
3. Giải thích các hiệu ứng trong hồi quy logistic
Xác suất bị giới hạn nghiêm trọng cho các mục đích ước tính và dự báo. Đầu tiên, chúng được giới hạn trong phạm vi từ 0 đến 1. Điều này có nghĩa là nếu ảnh hưởng thực tế của biến x đến kết quả của biến y vượt quá 1, thì việc giải thích có thể có vấn đề. Hạn chế thứ hai, xác suất không thể âm. Giả sử rằng biến độc lập có ảnh hưởng tiêu cực đến y, việc giải thích hệ số hồi quy logistic là vô nghĩa. Hệ số hồi quy chỉ có thể là số dương.
Làm thế nào để giải quyết hai vấn đề trên?
Có một phương pháp hai bước mà chúng tôi thực hiện hai phép biến đổi. Đầu tiên, chúng tôi chuyển đổi xác suất của tỷ lệ cược (o) thành:

Nghĩa là, xác suất của một sự kiện xảy ra là tỷ số giữa số lần sự kiện dự kiến xảy ra với số lần sự kiện dự kiến sẽ không xảy ra. Đây là mối quan hệ trực tiếp giữa tỷ lệ cược (y = 1) và xác suất y = 1. Do đó, cho rằng tỷ lệ cược có thể là vô hạn, xác suất của tỷ lệ cược bây giờ cho phép hệ số hồi quy có giá trị bất kỳ.
Bước tiếp theo là giải quyết vấn đề thứ hai. Mối quan hệ giữa tỷ lệ cược và xác suất, mở rộng một chút đại số, chúng ta có thể lập lại công thức trên cho tỷ lệ cược (o) theo lôgarit của tỷ lệ cược (y = 1):

Tính toán lôgarit của giá trị của một biến độc lập hoặc hiệp biến ngẫu nhiên trong tổng thể. Thêm giá trị 1 vào biến phụ thuộc y (ví dụ: 1 (bầu cho Obama năm 2008), 0 (bầu cho McCain năm 2008, trong cuộc bầu cử Hoa Kỳ), giả sử xác suất bỏ phiếu cho Obama p (y = 1) là 0,218 ; do đó, 1-p = 0,782 tỷ lệ cược chúng tôi nhận được là: tỷ lệ cược = 0,218 / 0,782 = 0,279 Đây chỉ là tỷ lệ cược mà chúng ta thấy, bây giờ chúng ta phải tiếp tục giả định các hướng hệ số hồi quy logistic liên quan đúng, vì vậy chúng ta cần sử dụng công thức logarit cho tỷ lệ cược.
Do đó, log tự nhiên (loge, ký hiệu ln) của tỷ lệ cược (ví dụ: ln 0,279 = -1,276). Vì vậy, logarit của xác suất bỏ phiếu cho Obama là ‘-1,276’. Vì vậy, nếu chỉ dừng lại ở những dự đoán xác suất, chúng ta có thể nhận được kết quả sai (số dương). Thứ hai, tác động thực sự của các hiệp biến liên quan bị đánh giá thấp. Ưu điểm chính của tỷ lệ cược log là các hệ số được giới hạn ở mức âm hoặc dương, nằm trong khoảng từ âm vô cùng đến dương vô cùng.
Như đã nói, hồi quy logistic trông giống hệt như hồi quy bội số ở phía bên phải của phương trình tỷ lệ cược log. Vế trái của phương trình không phải là một phần nhỏ của y. Nó là logarit của tỷ lệ cược (y = 1). Điều này có nghĩa là mọi đơn vị của x đều có ảnh hưởng β đến tỷ lệ cược log của y. Tỷ lệ cược log của y không phải là một khái niệm đơn giản, vì vậy chúng ta cần một cách khác để giải thích hiệu ứng trong hồi quy logistic, hãy đọc phần tiếp theo.
4. Ước tính mô hình hồi quy logistic với khả năng xảy ra tối đa
Bởi vì hồi quy logistic hoạt động trên các biến phân loại, phương pháp bình phương nhỏ nhất thông thường – ols không khả dụng (nó giả định một biến phụ thuộc phân phối chuẩn). Do đó, một công cụ ước lượng tổng quát hơn được sử dụng để phát hiện sự phù hợp tốt của các tham số. Đây được gọi là “ước tính khả năng xảy ra tối đa”.
Khả năng xảy ra tối đa là một kỹ thuật ước tính tương tác để chọn các ước tính tham số tối đa hóa khả năng quan sát tập dữ liệu mẫu. Trong hồi quy logistic, hệ số lựa chọn hợp lý tối đa ước tính, đối với một tập giá trị x nhất định, logarit của xác suất tối đa hóa xác suất quan sát một tập giá trị cụ thể của biến phụ thuộc trong mẫu.
Nhưng câu hỏi nghiên cứu cơ bản mà khả năng xảy ra tối đa sẽ giải quyết được là: giá trị tham số nào của dân số thực sự tạo ra mẫu mà chúng ta đang quan sát?
Vì hồi quy logistic sử dụng khả năng xảy ra tối đa, nên không thể ước tính hệ số xác định (r2) một cách trực tiếp. Do đó, cách giải thích của chúng ta về hồi quy logistic có hai tình huống khó xử: Thứ nhất, làm thế nào để chúng ta đo lường “mức độ phù hợp” – giả thuyết vô hiệu chung? Thứ hai, làm thế nào để chúng ta ước tính ảnh hưởng từng phần của mỗi biến x? Để trả lời câu hỏi này, hãy xem phần tiếp theo.
5. Suy luận thống kê và giả thuyết vô hiệu
Câu hỏi đầu tiên, làm cách nào để chúng tôi đo lường “mức độ phù hợp” – giả thuyết vô hiệu chung? Suy luận thống kê và giả thuyết vô hiệu được hiểu như sau:
– Bước đầu tiên trong việc giải thích một hồi quy là đánh giá giả thuyết rỗng tổng quát rằng các biến độc lập không có bất kỳ mối quan hệ nào với y. Trong phương pháp hồi quy ols, chúng tôi thực hiện điều này bằng cách sử dụng kiểm định f để kiểm tra xem r2 trong tổng thể có phải bằng 0 hay không. Trong khi hồi quy logistic sử dụng khả năng xảy ra tối đa (không có ols): giả thuyết vô hiệu h0 là: β0 = β0 = β0 = 0. Chúng tôi sử dụng thống kê log-khả năng xảy ra để đo kích thước còn lại của mô hình này.
– Sau đó, chúng ta ước lượng lại mô hình, giả sử giả thuyết rỗng là sai, chúng ta tìm giá trị hợp lý lớn nhất của hệ số β trong mẫu. Một lần nữa, chúng tôi sử dụng logarit thống kê về tính hợp lý để đo kích thước thặng dư của mô hình này.
– Cuối cùng, chúng tôi so sánh hai thống kê bằng cách tính toán thống kê thử nghiệm: -2 (ln lnull – ln lmodel)
Thống kê này cho họ biết có thể giảm bao nhiêu phần dư (hoặc sai số dự đoán) bằng cách sử dụng biến x. Giả thuyết rỗng nói rằng mức giảm này là 0; nếu thống kê đủ lớn (trong phép kiểm định chi bình phương với df = số biến độc lập), chúng tôi bác bỏ giả thuyết rỗng. Ở đây chúng tôi kết luận rằng ít nhất một biến độc lập có ảnh hưởng đến tỷ lệ cược log.
spss cũng sử dụng thống kê r2 để giúp đo lường sức mạnh của liên kết. Nhưng nó là một r2 giả và không nên được giải thích vì hồi quy logistic không sử dụng r2 như hồi quy tuyến tính.
Câu hỏi thứ hai, làm thế nào để chúng ta đánh giá tác động một phần của mỗi biến x?
Chúng tôi đánh giá tác động từng phần của các yếu tố dự đoán khi giả thuyết vô hiệu chung bị bác bỏ.
Cũng như trong hồi quy tuyến tính bội số, trong hồi quy logistic, điều này có nghĩa là giả thuyết rỗng cho mỗi biến độc lập được đưa vào phương trình. Giả thuyết rỗng cho mỗi hệ số hồi quy bằng 0 hoặc nó không ảnh hưởng đến tỷ lệ cược log.
Mỗi công cụ ước lượng hệ số b có một sai số chuẩn – trung bình, cách chúng tôi mong đợi b thay đổi ngẫu nhiên từ mẫu này sang mẫu khác. Để kiểm tra mức độ quan trọng của b, hãy tính một thống kê kiểm định (không phải kiểm định t, mà là một chi-bình phương wald) với 1df bậc tự do. Cần nhớ rằng hệ số b đại diện cho ảnh hưởng của sự thay đổi đơn vị trong x đối với tỷ lệ cược log.
Trong giáo dục, hiệu quả là tích cực, với tỷ lệ cược log tăng theo trình độ học vấn.
Giá trị exp (b) của biến độc lập x được sử dụng để dự đoán xác suất của một sự kiện dựa trên sự thay đổi một đơn vị trong biến độc lập với tất cả các biến độc lập khác được giữ cố định. Nó đại diện cho khi Nó được tăng lên một và tỷ lệ cược của sự kiện là “có” được nhân với giá trị của giá trị exp (b) (đây là hàm e được nâng lên lũy thừa b, giả sử 1,05, tăng 5%).
6. Hồi quy logistic mở rộng
Phía bên phải của phương trình hồi quy logistic tương tự như bất kỳ mô hình hồi quy nào khác, vì vậy chúng tôi có thể bao gồm cả các biến độc lập phân loại và liên tục trong hồi quy logistic. Chúng tôi cũng có thể bao gồm các hiệu ứng tương tác.
Hồi quy hậu cần có thể được mở rộng theo hai cách:
– Hồi quy logistic thông thường được sử dụng để phân tích logarit tích lũy của tỷ lệ thắng xếp hạng cao nhất tiếp theo cho một biến thứ tự tổng hợp. Một ví dụ điển hình là Khảo sát về thái độ, có thể chọn giữa “Rất không đồng ý, Không đồng ý, Trung lập, Đồng ý, Rất đồng ý”. Chúng ta có thể sử dụng hồi quy logistic phân cấp để kiểm tra xem x có tăng thêm một đơn vị hay không, tỷ lệ cược đăng nhập của việc chọn “không đồng ý” so với “hoàn toàn đồng ý” hoặc “đồng ý” so với “trung lập”.
– Hồi quy Logistic Đa thức Các danh mục nhiều lựa chọn để phân tích kết quả. Ví dụ, chúng tôi muốn dự đoán xem một người đã kết hôn, ly hôn, ly thân, chưa kết hôn. Nếu nó loại trừ lẫn nhau và tập thể, chúng ta có thể phân tích lô-ga-rít tỷ lệ cược của mỗi kết quả so với đường cơ sở. Ví dụ, chúng ta có thể thực hiện phân tích logarit về tỷ lệ kết hôn so với chưa bao giờ kết hôn, ly hôn so với chưa bao giờ kết hôn và ly thân so với chưa bao giờ kết hôn. Chúng ta có thể kiểm tra các giả thuyết về tác động của các yếu tố dự đoán đối với mỗi tỷ lệ cược này. Mô hình hồi quy logistic đa thức Sau đó, hãy kiểm tra đa thức danh nghĩa.
7. Giả thuyết thử nghiệm
Các giả định cơ bản của hồi quy logistic nhị thức bao gồm:
– Biến phụ thuộc của bạn phải được đo lường trên thang đo nhị phân. Ví dụ về các biến nhị phân bao gồm giới tính (nam và nữ), điểm kiểm tra (đạt và không đạt), loại tính cách (hướng nội hoặc hướng ngoại), v.v. Tuy nhiên, nếu biến phụ thuộc của bạn được đo lường trên thang đo liên tục, bạn sẽ cần thực hiện hồi quy tuyến tính nhiều lần, trong khi nếu biến phụ thuộc của bạn được đo lường trên thang đo thứ tự, thì bước hồi quy logistic thứ hai sẽ thích hợp hơn.
– Một hoặc nhiều biến độc lập, có thể liên tục (tức là khoảng hoặc tỷ lệ) hoặc phân loại (tức là thứ tự hoặc danh nghĩa). Ví dụ về các biến số liên tục bao gồm thời gian ôn tập (tính bằng giờ), trí thông minh (tính theo chỉ số IQ), điểm kiểm tra (theo thang điểm từ 0 đến 100), v.v. Ví dụ về biến thứ tự bao gồm các mục likert (ví dụ: thang điểm 5 hoặc 7 từ “rất đồng ý” đến “rất không đồng ý”). Ví dụ về các biến danh nghĩa bao gồm giới tính (nam và nữ), khu vực cư trú (thành thị và nông thôn), nghề nghiệp (ví dụ 5 nhóm: điện, nó, cơ khí, ngoại ngữ, kinh tế).
– Các quan sát là độc lập và biến phụ thuộc phải có các danh mục hoàn chỉnh và loại trừ lẫn nhau.
– Cần có một mối quan hệ tuyến tính giữa phép biến đổi logit (còn được gọi là logit) của bất kỳ biến độc lập liên tục nào và biến phụ thuộc. Chúng ta có thể sử dụng thủ tục box-tidwell (1962) để kiểm tra tính tuyến tính của giả định này.
Bạn có thể kiểm tra Giả thuyết 4 bằng cách sử dụng thống kê spss. Các giả thuyết 1, 2 và 3 nên được kiểm tra trước trước khi chuyển sang Giả thuyết 4. Bạn nên kiểm tra các giả thuyết này theo thứ tự này vì nó đại diện cho một thứ tự. Nếu bạn không chạy chính xác các thử nghiệm thống kê trên các giả định này, bạn có thể nhận được kết quả không hợp lệ khi chạy hồi quy logistic nhị thức.
8. Phân tích hồi quy logistic nhị thức trong spss
Ví dụ: chúng tôi có thể sử dụng hồi quy logistic nhị thức để xem liệu điểm kiểm tra toán của học sinh có thể được dự đoán dựa trên thời gian ôn tập, mức độ lo lắng và điểm yếu của bài kiểm tra hay không. Yếu tố giới tính (nghĩa là, biến phụ thuộc là ‘điểm kiểm tra’, được đo trên thang điểm lưỡng phân ‘đạt’ hoặc ‘không đạt’ và ba biến độc lập: ‘thời gian xem xét’ và ‘giới tính’). Hai mươi học sinh đã được mời tham gia vào một thí nghiệm, trong đó họ được yêu cầu ghi lại tổng số giờ ôn tập (tích lũy mỗi ngày) môn toán từ cuối lớp giải tích cho đến ngày thi cuối kỳ. Vào cuối kỳ thi, các nhà nghiên cứu thu thập điểm của 20 sinh viên này trên thang điểm 10 (đạt ‘1’ nếu ≥5, không đạt ‘0’ nếu <5), gán các giá trị 1 = nam, 2 = nữ. Dữ liệu được tóm tắt trong bảng dưới đây.

Các bước của phân tích hồi quy logistic nhị phân trong spss như sau:
Bước 1: Chọn Phân tích & gt; Hồi quy & gt; Hậu cần kép …

Bước 2: Trong hộp thoại Hồi quy logistic, chúng tôi di chuyển biến phụ thuộc ‘ diemthi ‘ vào hộp phụ thuộc bằng các biến độc lập đặt ‘ gioitinh ‘, ‘ ontap ‘ làm hiệp biến .

Bước 3: Nhấp vào nút Phân loại để mở hộp thoại Hồi quy logistic: Xác định các biến phân loại . Chuyển đổi “ gioitinh ” từ cùng các hộp hiệp biến độc lập phân loại thành hộp hiệp biến phân loại . Trong vùng Thay đổi độ tương phản , chúng tôi thay đổi “ cuối cùng ” thành “ nắm tay ” và nhấp vào thay đổi . Sau đó, nhấp vào Tiếp tục .

Bước 4: Nhấp vào nút Tùy chọn để mở hộp thoại Hồi quy hậu cần: Tùy chọn . Trong khu vực thống kê và lô , chúng tôi chọn lô phân loại, hosmer-lemeshow độ tốt của sự phù hợp, danh sách phần còn lại và ci cho exp (b) Strong>. Trong vùng Hiển thị , nhấp vào ở bước cuối cùng . Sau đó, nhấp vào Tiếp tục .
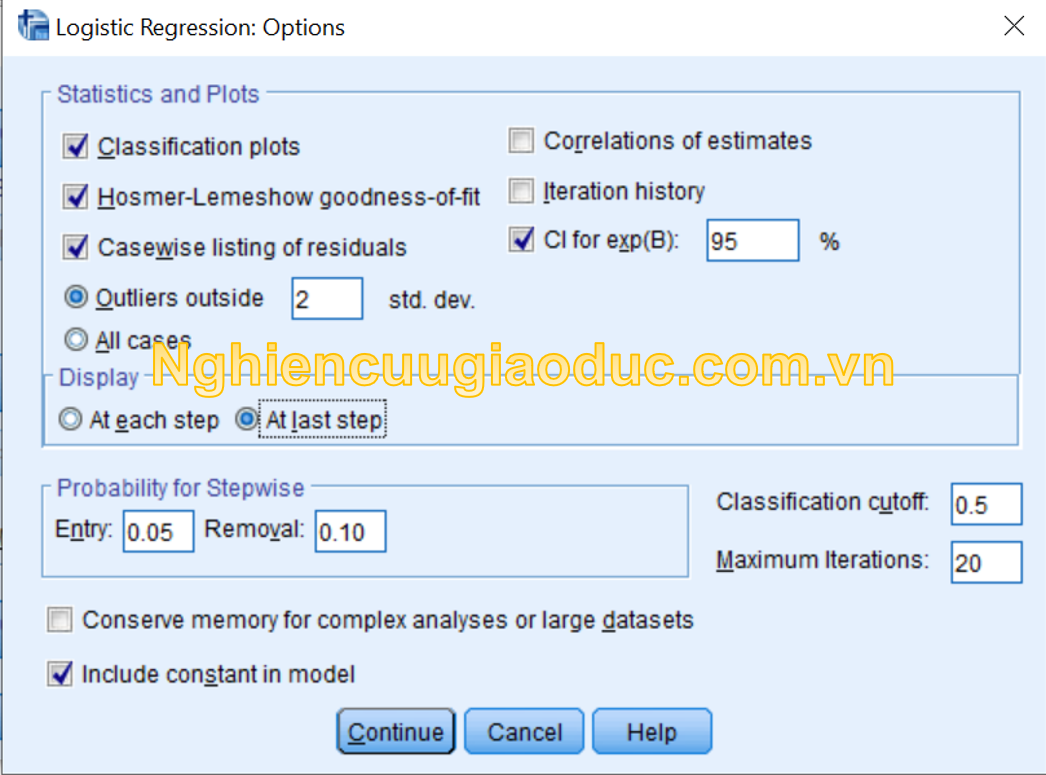
Bước 5: Nhấp vào ok để chạy kết quả.
Đọc kết quả:
Nói chung, hồi quy logistic sử dụng nhiều bảng, nhưng chúng tôi có thể muốn xem xét các bảng chính sau:

Bảng Tóm tắt Xử lý Trường hợp cung cấp cho chúng tôi thông tin mô tả các đặc điểm của dữ liệu được đưa vào phân tích hồi quy logistic nhị phân. 20 quan sát được đưa vào phân tích ( bao gồm trong phân tích ), không bị thiếu ( trường hợp thiếu ), không được chọn ( trường hợp thiếu ) mạnh> ) trường hợp không được chọn ).
Tiếp theo, chúng tôi bỏ qua phần khối 0 vì kết quả phân tích ở đây không có các biến độc lập được đưa vào mô hình. Chúng tôi sẽ sử dụng kết quả từ khối 1, có tính đến tất cả các biến độc lập.

Bảng đầu tiên là Kiểm tra toàn diện các hệ số của mô hình . Bảng hiển thị các hệ số của mô hình. Bước 1 là bước đầu tiên để chạy mô hình logic. Vì ở đây ta sử dụng phương pháp enter để đưa đồng thời các biến độc lập nên chỉ xuất hiện bước 1 trong kết quả thống kê. Trong trường hợp các phương pháp khác, bảng này sẽ có thêm các bước 2, 3, 4 tùy thuộc vào số lượng biến được đưa vào. Phương thức enter mang lại 3 giá trị chi-square, df và sig. Các bước, khối và mô hình giống nhau. Trong mọi trường hợp p = 0,001 <0,05 nên mô hình hồi quy có ý nghĩa thống kê.

Bảng
Tóm tắt Mô hình trình bày các kết quả tóm tắt về sự phù hợp của mô hình. Cột -2 log-khả năng xảy ra (được biểu thị bằng -2ll) là tham số xem xét so sánh giữa các mô hình hồi quy và -2ll của mô hình càng nhỏ thì càng tốt . Nhưng nó không có nhiều ý nghĩa nếu không so sánh với các mô hình hồi quy khác.
Hai cột cox & amp; snoll r square và nagelkerke r square là các giá trị r2 giả. Hồi quy logistic không sử dụng cùng giá trị r2 như hồi quy tuyến tính. Cũng giống như -2ll , hai số liệu này được sử dụng để so sánh các mô hình hồi quy khác nhau trên cùng một tập dữ liệu và cùng một biến phụ thuộc. Một mô hình hồi quy tốt hơn sẽ có r2 lớn hơn.

Kết quả thử nghiệm thử nghiệm hosmer và lemeshow cho biết sự phù hợp của mô hình hồi quy tổng thể. Giá trị p nhỏ (thường nhỏ hơn 5%) có nghĩa là mô hình đó không phù hợp. Nhưng giá trị p lớn không nhất thiết có nghĩa là mô hình của bạn phù hợp, chỉ là không có đủ bằng chứng cho thấy nó không phù hợp. Nhiều tình huống dẫn đến giá trị p lớn, bao gồm cả sức mạnh thống kê kém. Tiêu thụ điện năng thấp là một trong những lý do khiến thử nghiệm này bị chỉ trích. Trong ví dụ này, p = 0,93> 0,05 có nghĩa là mô hình hồi quy phù hợp, tức là mô hình hồi quy tổng thể được chấp nhận.
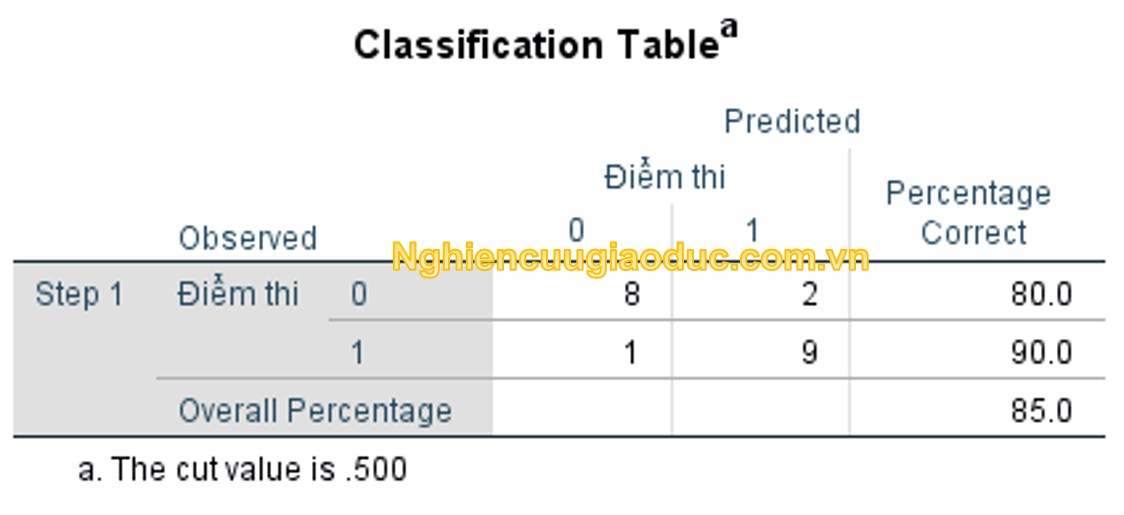
Bảng phân loại hiển thị xác suất được dự đoán (đạt) so với điểm kiểm tra quan sát thực tế. Giá trị ngưỡng 0,5 có nghĩa là spss phân loại một sự kiện là đã xảy ra (tức là đã vượt qua, đã vượt qua bài kiểm tra) nếu xác suất ước tính của sự kiện xảy ra lớn hơn hoặc bằng 0,5. Nếu xác suất nhỏ hơn 0,5, spss phân loại sự kiện là không xảy ra (kiểm tra không thành công). Do đó, trong số 10 trường hợp quan sát thực tế không thành công thì có 8 trường hợp dự đoán là thất bại, với tỷ lệ dự đoán đúng là 8/10 = 80%. Đã đạt (qua bài test) trong 10 trường hợp quan sát thực tế, dự đoán 9 trường hợp đậu, tỷ lệ dự đoán đúng là 9/10 = 90%. Do đó, độ chính xác dự đoán trung bình là (10 * 80 + 10 * 90) = 85%.

Bảng
Các biến trong phương trình cung cấp nhiều thông tin về phương trình hồi quy. Kiểm tra wald (cột “ wald “) được sử dụng để xác định ý nghĩa thống kê của từng biến độc lập. Ý nghĩa thống kê của thử nghiệm nằm trong cột “ sig. “. Đặc biệt trong trường hợp này, giá trị p của kiểm định Wald cho các biến ‘gioitinh’, ‘ontap’ nhỏ hơn 0,05 (độ tin cậy 95%) cho thấy nó có ảnh hưởng đáng kể đến mô hình dự đoán biến diemthi. Nếu giá trị của bất kỳ biến độc lập nào là p>; 0,05 thì nó chỉ ra rằng nó không ảnh hưởng đến biến phụ thuộc. Trong ví dụ này, các biến ‘gioitinh’ và ‘ontap’ đều ảnh hưởng đến dự đoán của học sinh đối với biến ‘diemthi’.
Giá trị cột exp (b) được sử dụng để dự đoán xác suất của một sự kiện dựa trên sự thay đổi đơn vị của biến độc lập, tất cả các cài đặt khác của biến độc lập được giữ không đổi. Ví dụ, bảng cho thấy tỷ lệ học sinh thi đỗ (loại “Đạt”) cao hơn nam 20,345 lần và nữ cao hơn 20,345 lần. Tức là, phụ nữ có khả năng vượt qua bài kiểm tra cao hơn 20,345 lần so với nam giới, với khoảng tin cậy là 1,209 – 342,554. Khoảng tin cậy này quá rộng, có thể là do kích thước mẫu nhỏ và câu hỏi có nhiều thông tin hơn.
Cột b là hệ số hồi quy của biến độc lập. Nếu b là dấu âm có nghĩa là ảnh hưởng của biến độc lập đến biến phụ thuộc là âm, ngược lại, b là dấu dương cho thấy biến độc lập có ảnh hưởng tích cực đến biến phụ thuộc. Các biến độc lập có p> trường hợp; 0,05 trong kiểm định của Wald sẽ không được đưa vào phương trình hồi quy. Phương trình hồi quy thu được là:

Do đó, thời gian ôn tập nhiều sẽ làm tăng khả năng đậu và học sinh nữ dễ đậu hơn học sinh nam.
Một lợi thế rất mạnh của hồi quy logistic nhị thức là khả năng dự đoán. Ví dụ, một sinh viên nữ có thời gian ôn tập là 5 giờ, hãy thay thế phương trình sau:

Trong khi vẫn còn 5 giờ ôn tập, xác suất này đối với học sinh nam sẽ là:

Do đó, xác suất trong cả hai trường hợp đều lớn hơn 50%. Tức là nếu học 5 tiếng thì khả năng đậu của học sinh khá lớn (> 0,5).
9. Kiểm định giả thuyết hồi quy về mối quan hệ tuyến tính giữa biến độc lập liên tục và biến phụ thuộc logit
Phương pháp 1: Vẽ biểu đồ mối quan hệ giữa các biến độc lập liên tục và xác suất dự đoán p
Bước 1: Chọn Phân tích & gt; Hồi quy & gt; Hậu cần kép …
Bước 2: Trong hộp thoại Hồi quy logistic, chúng tôi di chuyển biến phụ thuộc ‘ diemthi ‘ vào hộp phụ thuộc bằng các biến độc lập đặt ‘ gioitinh ‘, ‘ ontap ‘ làm hiệp biến .
Bước 3: Nhấp vào nút Lưu và chọn hộp xác suất (đây là xác suất dự đoán của diemthi ). Nhấp vào Tiếp tục , sau đó nhấp vào ok để chạy kết quả.
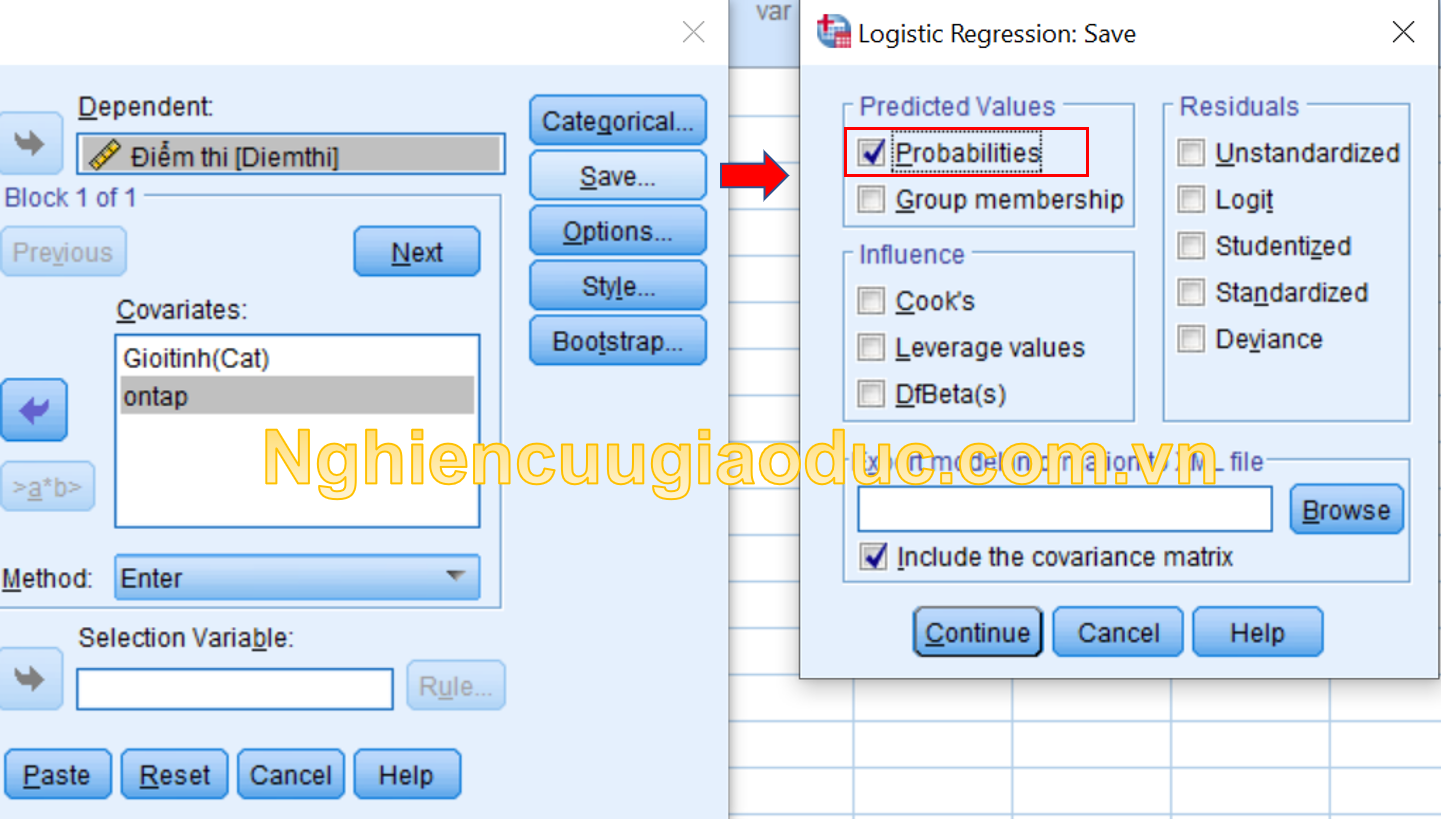
Kết quả: Trong tệp dữ liệu có cột trước 1 là xác suất dự đoán diemthi của học sinh.

Bây giờ chúng ta tiến hành vẽ biểu đồ mối quan hệ giữa biến diemthi (trục y) và biến độc lập liên tục “ontap” (trục x). Vui lòng đọc Hướng dẫn vẽ đồ thị phân tán để biết hướng dẫn vẽ đồ thị.

Do đó, biểu đồ biểu thị một đường thẳng xuyên qua đám mây phân đoạn. Điểm số cũng cách đều so với đường cơ sở, cho thấy hiệp phương sai. Mặc dù kích thước mẫu quá nhỏ để có thể thấy rõ mối quan hệ tuyến tính giữa biến ontap và xác suất dự đoán diemthi của học sinh. Nhưng kích thước mẫu lớn hơn sẽ quan sát rõ ràng độ tuyến tính. Do đó, giả định rằng có một mối quan hệ tuyến tính giữa biến liên tục “ontap” và xác suất dự đoán p được thỏa mãn.
Phương pháp 2: Checkbox-tidwell
Mặc dù hồi quy logistic thường được coi là không có giả thuyết, chúng tôi giả định rằng mối quan hệ giữa các yếu tố dự đoán liên tục và logit (tỷ lệ cược log) là tuyến tính. Giả thuyết này có thể được kiểm tra bằng cách bao gồm sự tương tác giữa các yếu tố dự đoán liên tục và logarit của chúng. Nếu sự tương tác này là đáng kể, thì giả thuyết bị vi phạm. Tôi nên cảnh báo với bạn rằng kích thước mẫu cũng là một yếu tố, vì vậy bạn không nên lo lắng quá nhiều về các tương tác đáng kể khi kích thước mẫu lớn. Nếu không có tương tác nhật ký quan trọng nào, nó sẽ bị xóa khỏi mô hình, báo cáo giả định không có vấn đề gì và kết quả của mô hình được trình bày mà không có thuật ngữ tương tác nhật ký.
Dưới đây, chúng tôi trình bày cách tạo logarit tự nhiên (ln) của một công cụ dự đoán liên tục. Nếu công cụ dự đoán có giá trị từ 0 trở xuống, trước tiên hãy thêm một hằng số vào mỗi điểm sao cho không có giá trị nào bằng 0 hoặc nhỏ hơn. Hình ảnh dưới đây cho thấy cách nhập hiệu ứng tương tác. Trong ngăn bên trái, chọn hai yếu tố dự đoán để đưa vào tương tác và nhấp vào & gt; a * b & gt; . nút
– Bước 1: Biến đổi logarit tự nhiên với biến liên tục “ontap”. Nhấp vào Biến đổi & gt; Biến được tính để mở hộp thoại Biến được tính. Nhập tên biến mới ontapln vào trường Biến mục tiêu. Sau đó nhập hàm logarit tự nhiên (ln) với giá trị ontap, như hình dưới đây:

– Bước 2: Thêm hiệu ứng giữa các biến ontap và ontapln trong mô hình hồi quy. Trong hộp thoại Hồi quy hậu cần , nhấp vào thiết bị đầu cuối ontap và biến ontapln, sau đó nhấp vào nút & gt; a * b & gt; . Cuối cùng, chạy lại mô hình hồi quy.

– Bước 3: Đọc kết quả trong bảng Các biến trong phương trình

Do đó, tương tác của “ontapln theo đánh giá” là không có ý nghĩa (p = 0,204> 0,05). Nếu tương tác là đáng kể, chúng tôi sẽ cố gắng tăng cường độ mô hình của các yếu tố dự đoán (tức là sẽ là đa thức).
Tài liệu tham khảo
- coolican, h. (2018). Phương pháp nghiên cứu tâm lý và thống kê. Routledge.
- hanneman, r. a., kposowa, a. j., & amp; riddle b. d. (2012). Thống kê cơ bản cho nghiên cứu xã hội (Tập 38). John Wiley các con trai.
- Jackson, s. l. (2015). Phương pháp nghiên cứu và thống kê: Phương pháp tư duy phản biện. Tham gia học tập.
- mcqueen, r. A, & amp; Knudsen, P. (2006). Giới thiệu về phương pháp nghiên cứu và thống kê trong tâm lý học. Giáo dục Pearson.
- Đồng đẳng, tức là. (năm 2006). Phân tích thống kê cho các nhà nghiên cứu tâm lý và giáo dục: Công cụ cho các nhà nghiên cứu tâm lý và giáo dục. Routledge.



