Hình nón nói chung và hình chóp tứ diện nói riêng là một phần của hình học trong học kì 2 môn Toán lớp 8. Sau đây là phần tóm tắt định nghĩa, tính chất, công thức tính Hình chóp là gì Tính chu vi, diện tích, thể tích của hình chóp? Ngoài ra, chúng tôi còn bổ sung những kiến thức về hình chóp mà trong sách giáo khoa ít đề cập đến.
Hình chóp là gì?
Xác định”
- Hình chóp là hình học không gian, đáy là đa giác lồi, các mặt bên đều là tam giác, tổng cộng có một đỉnh gọi là đỉnh của hình chóp
- Có nhiều loại kim tự tháp, tên của chúng được xác định theo cơ sở.
- Hình chóp tam giác có đáy là tam giác và hình chóp tứ giác có đáy là tứ giác.
- Trường hợp đặc biệt đáy là tam giác đều hoặc tứ giác đều thì ta gọi là hình chóp đều
- Đường thẳng đi qua khối chóp và vuông góc với mặt đáy gọi là đường cao của hình chóp.
- Tên gọi của hình chóp dựa trên hình dạng đa giác của đáy: hình chóp có đáy là hình tam giác gọi là hình chóp tam giác, hình chóp có đáy là hình tứ giác được gọi là hình tứ giác.
- Nếu các mặt bên của hình chóp đều hoặc cạnh đáy thì chiều cao của đáy là tâm đường tròn ngoại tiếp đáy.
- Nếu các cạnh của một hình chóp tạo với đáy một góc bằng nhau hoặc nếu chiều cao từ đỉnh đến các cạnh bằng nhau thì đáy của đường cao là tâm của đường tròn nội tiếp trên đáy.
- Nếu một hình chóp có một cạnh hoặc đường chéo vuông góc với mặt đáy thì chiều cao của hình chóp sẽ bằng chiều cao của cạnh hoặc đường chéo đó.
- Hình chóp tam giác đều có ba mặt phẳng đối xứng
- Kim tự tháp có đáy là tam giác đều
- Cả hai bên đều bình đẳng
- Tất cả các cạnh là tam giác đều
- Chân cao trùng với tâm mặt đáy (tâm mặt đáy là tâm tam giác)
- Tất cả các cạnh và đáy tạo thành các góc bằng nhau
- Các cạnh và đáy tạo thành các góc bằng nhau
- Kim tự tháp có đáy vuông
- Cả hai bên đều bình đẳng
- Tất cả các cạnh là tam giác đều
- Chân mặt ngoài trùng với tâm mặt đáy (tâm mặt đáy là giao điểm của 2 đường chéo)
- Các cạnh và đáy tạo thành các góc bằng nhau
- Hình chóp tứ giác có 8 cạnh
- Mỗi cạnh của hình chóp cụt là một hình thang cân
- p là nửa cuối tuần
- d là trung điểm của hình chóp. Trung điểm là chiều cao từ đỉnh đến trung điểm của cạnh.
- s là vùng dưới cùng,
- h là chiều cao
- b’ và b lần lượt là diện tích đáy nhỏ và diện tích đáy lớn của hình chóp cụt đều.
- h là chiều cao (khoảng cách giữa hai đáy).
- Sử dụng quan hệ song song và vuông góc giữa đường thẳng và mặt phẳng.
- Kiến thức sử dụng kim tự tháp quy tắc
Tính chất của hình chóp:
Các loại kim tự tháp phổ biến
Thế nào là hình chóp tam giác đều?
*Định nghĩa:
Hình chóp tam giác đều là hình chóp có đáy là tam giác đều và mặt bên là tam giác đều có đáy chung
*Tính năng
***Lưu ý:
Tâm của tam giác đều là giao điểm của 3 đường trung tuyến đồng thời là đường phân giác của đường cao, đường phân giác vuông và đường phân giác trong.
Thế nào là hình chóp tứ giác đều?
*Định nghĩa:
Hình chóp tứ giác đều là hình chóp có đáy là hình vuông và các mặt bên là các tam giác cân có chung một đỉnh
*Tính năng
Hình chóp cụt là gì?
*Định nghĩa:
Hình chóp cụt đều là hình chóp đều cắt bởi một mặt phẳng song song với mặt đáy. Phần hình chóp nằm giữa mặt phẳng này và mặt phẳng đáy của hình chóp được gọi là hình chóp cụt
*Thuộc tính:
Công thức tính chu vi, diện tích, thể tích hình chóp
Công thức tính chu vi hình chóp (áp dụng cho hình chóp tam giác và tứ giác)
Chu vi hình chóp bằng tổng chu vi các đáy
Công thức:
p = đáy + cạnh
Ở đó
đáy là chu vi của đáy
Cạnh là chu vi của một cạnh
Công thức tính diện tích hình chóp đều (áp dụng cho hình chóp tam giác và hình chóp tứ giác)
Diện tích hình chóp bao gồm diện tích xung quanh và diện tích toàn phần.
Khu vực xung quanh
Diện tích của hình chóp đều bằng tích của nửa đường tròn đáy và trung điểm
Công thức nấu ăn
sxq = p.d
Ở đâu:
Tổng diện tích Kim tự tháp:
Diện tích toàn phần của hình chóp bằng tổng diện tích xung quanh và diện tích đáy
stp = sxq + đáy
Vì vậy, để tính diện tích xung quanh và diện tích toàn phần của hình chóp ta cần tính độ dài và chu vi của phần giữa và diện tích của mặt đáy.
Thể tích hình nón (áp dụng cho hình chóp tam giác và tứ giác)
Công thức nấu ăn
v=1/3s.h
Ở đâu:
Thể tích của hình chóp tứ giác
Công thức:
Ở đâu:
Hình tháp khác biệt
Bài tập kim tự tháp
Xác định mối liên hệ giữa các cạnh và các yếu tố của mặt phẳng trong hình chóp đều và hình chóp đều.
Bài tập ví dụ:
Bài tập 1: Cho hình chóp sabc có sa vuông góc với mặt phẳng (abc) và đáy abc là tam giác vuông tại b, ab = a, sa = a. Gọi h là hình chiếu của a trên cạnh sb. Khoảng cách giữa ah và bc bằng bao nhiêu?

Trả lời:
Ta có bc⊥ab và bc⊥sa→bc⊥(sab)→bc⊥hb
trong đó ah⊥hb→hb là đường vuông góc chung của ah và bc→d(ah,bc)=hb
Tam giác vuông cân sa=sb=a, ah⊥sc
→
poster 2: Cho hình chóp s abcd có đỉnh là tứ giác đều, các cạnh bên là tam giác đều, ab=8m, o là trung điểm của ac. Hình chóp abcd có bao nhiêu mặt? Độ dài là gì?
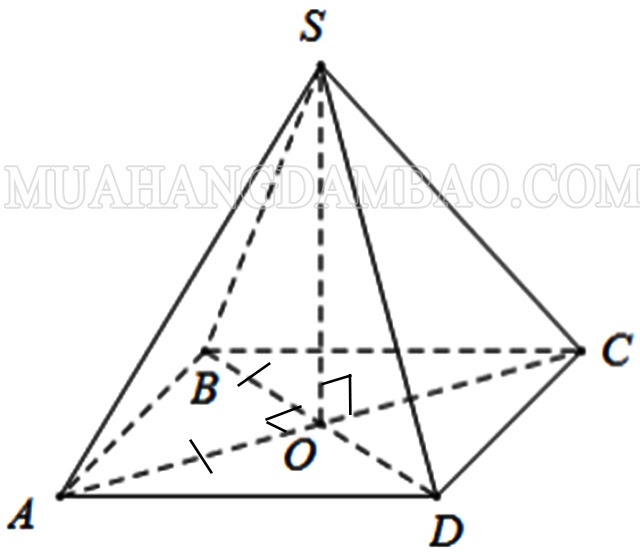
Trả lời:
s abcd là tứ giác có 8 cạnh
Hình nón s abcd đều nên đáy abcd là hình vuông oab vuông góc với o
Áp dụng định lý Pitago cho tam giác vuông oab ta có
ab2 = ob2+ ob2 → ab2 = 2oa2
Các cạnh của hình nón là tam giác đều nên Δsab là tam giác đều. Vậy sa = ab = 8m
Chúng ta có một hình vuông vì vậy chúng ta nên bình phương tại o
Áp dụng định lý Pitago cho tam giác vuông, ta có:
sb2 = os2+ oa2
Mong rằng qua phần tổng hợp kiến thức về hình chóp trên đây, các bạn đã hiểu và ghi nhớ các công thức tính chu vi, diện tích, thể tích hình chóp cũng như sự khác nhau giữa các loại hình chóp. . Chúc các em có một tiết học ấm áp và bổ ích.



