svm là một thuật toán giám sát có thể được sử dụng để phân loại hoặc đệ quy. Nhưng nó chủ yếu được sử dụng để phân loại. Trong thuật toán này, chúng tôi vẽ dữ liệu dưới dạng các điểm n chiều (trong đó n là số đối tượng địa lý bạn có) và giá trị của mỗi đối tượng địa lý sẽ là một phần của liên kết. Sau đó, chúng tôi thực hiện khám phá “siêu phẳng” của các lớp được phân vùng. Siêu phẳng được hiểu đơn giản là một đường thẳng có thể chia một lớp thành hai phần độc lập.
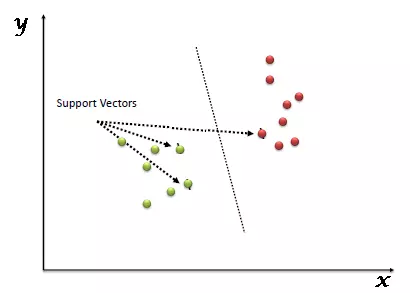
Vectơ hỗ trợ được hiểu đơn giản là quan sát các đối tượng trên bản đồ tọa độ và máy vectơ hỗ trợ là ranh giới tốt nhất để phân chia hai loại.
Ở trên, chúng ta đã thấy sự phân chia siêu phẳng. Vậy làm thế nào để chúng ta định nghĩa “cách vẽ – định nghĩa siêu phẳng”. Chúng tôi sẽ tuân theo các tiêu chuẩn sau:
- Xác định đúng siêu phẳng (tình huống 1):
- Xác định đúng siêu phẳng (tình huống 2):
- Xác định đúng siêu phẳng (tình huống 3):
- Chúng ta có thể phân loại hai lớp (tình huống 4) không?
- Tìm siêu phẳng chia thành các lớp (Tình huống 5)
- Xử lý không gian số chiều cao: Máy vector hỗ trợ là công cụ tính toán không gian số chiều cao hiệu quả, đặc biệt phù hợp với bài toán phân loại văn bản và phân tích ý kiến có kích thước cực lớn.
- Tiết kiệm bộ nhớ: Vì chỉ một tập hợp con các điểm được sử dụng trong đào tạo thực tế và ra quyết định trên các điểm dữ liệu mới, nên chỉ những điểm cần thiết mới được lưu trữ trong bộ nhớ tại thời điểm quyết định.
- Tính linh hoạt – Việc phân loại thường phi tuyến tính. Khả năng ứng dụng hạt nhân mới cho phép linh hoạt giữa các phương pháp tuyến tính và phi tuyến tính, dẫn đến hiệu suất phân loại được cải thiện.
- Vấn đề mang tính số cao: Nếu số thuộc tính (p) của tập dữ liệu lớn hơn nhiều so với số dữ liệu (n) thì svm cho kết quả kém.
- Xác suất không rõ ràng: việc phân loại svm chỉ cố gắng chia đối tượng thành hai lớp được phân tách bằng siêu phẳng svm. Điều này không tính đến khả năng một thành viên xuất hiện trong một nhóm. Tuy nhiên, hiệu quả của việc phân loại có thể được xác định theo khái niệm lề từ các điểm dữ liệu mới đến siêu phẳng phân lớp mà chúng ta đã thảo luận ở trên.
- https://machinelearningcoban.com/2017/04/09/smv/
- https://en.wikipedia.org/wiki/support_vector_machine
- https://medium.com/machine-learning-101/chapter-2-svm-support-vector-machine-theory-f0812effc72
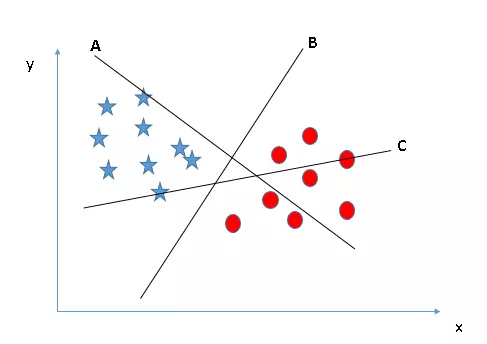
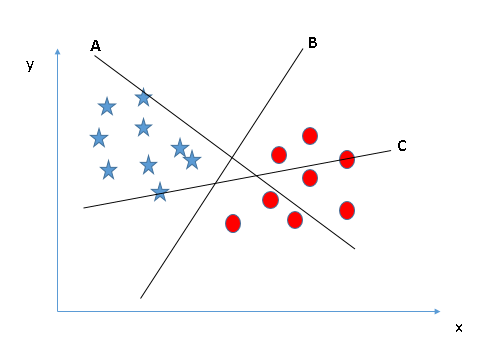
Có 3 siêu kênh (a, b và c). Bây giờ là làn đường vượt chính xác cho nhóm ngôi sao và vòng tròn.
Quy tắc đầu tiên chọn một siêu đường và chọn một siêu phẳng phân cách tốt nhất hai lớp. Trong ví dụ này dòng b.
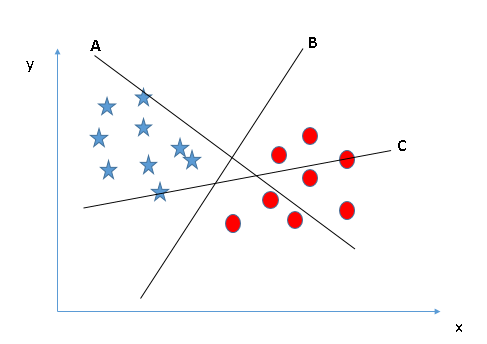
Ở đây ta cũng có 3 đường siêu phẳng (a, b, c) thỏa mãn quy tắc 1.
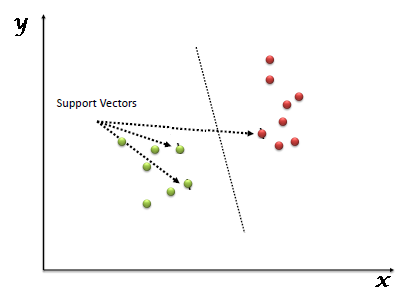
Quy tắc thứ hai là xác định khoảng cách tối đa từ điểm gần nhất của một lớp nhất định đến siêu phẳng. Khoảng cách này được gọi là “lề”, như thể hiện trong hình bên dưới, trong đó khoảng cách lề lớn nhất là đường c. Hãy nhớ rằng nếu bạn chọn sai siêu kênh có lề thấp hơn, rất có thể bạn sẽ xác định sai lớp cho dữ liệu của mình sau này khi dữ liệu tăng lên.
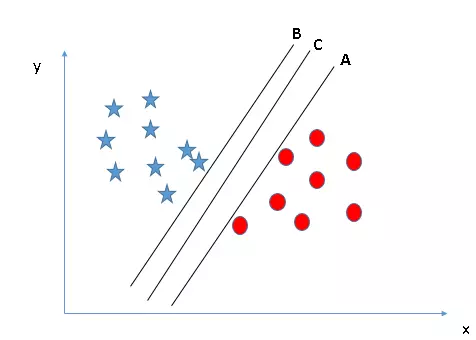
Sử dụng các nguyên tắc trên để chọn một siêu phẳng cho:
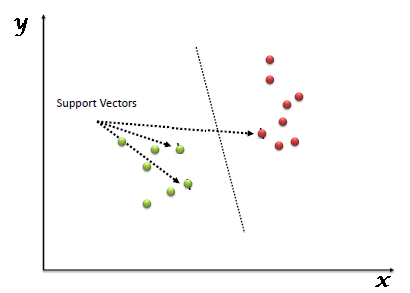
Có thể một số người sẽ chọn hàng b vì nó có lợi nhuận cao hơn hàng a, nhưng không phải vậy vì quy tắc đầu tiên sẽ là quy tắc #1 và chúng ta cần chọn siêu phẳng để phân tích các lớp riêng lẻ. Vì vậy, con đường a là sự lựa chọn chính xác.
Tiếp theo các bạn xem hình bên dưới, bạn không thể chia thành 2 layer riêng biệt bằng 1 dòng, tạo ra một phần chỉ có các ngôi sao và một vùng chỉ có các dấu chấm.
Ở đây, người ta sẽ chấp nhận rằng các ngôi sao bên ngoài được coi là nhiều ngôi sao bên ngoài hơn, svm có các thuộc tính cho phép bỏ qua các ngoại lệ và tìm siêu phẳng có giới hạn lớn nhất. Vì vậy, có thể nói rằng svm có khả năng chấp nhận ngoại lệ mạnh mẽ.
Trong ví dụ bên dưới, không tìm thấy siêu phẳng tương đối nào để phân chia các lớp, vậy làm thế nào để svm chia dữ liệu thành hai lớp riêng biệt? Cho đến nay chúng ta mới chỉ nghiên cứu các đường thẳng siêu phẳng.
svm có thể giải quyết vấn đề này, nó rất đơn giản, nó có thể được giải quyết bằng cách thêm một tính năng, ở đây chúng tôi thêm tính năng z = x^2+ y^2. Dữ liệu lúc này sẽ được chuyển đổi trên trục x và z như sau
Trong biểu đồ trên, những điểm chính cần xem xét là: • Tất cả dữ liệu trên trục z sẽ dương vì nó là tổng bình phương của x và y • Trên biểu đồ, vòng tròn màu đỏ xuất hiện càng nhiều thì y càng lớn. gần trục x, z càng nhỏ => gần trục x hơn trong đồ thị (z,x) trong svm, dễ dàng có một siêu phẳng tuyến tính được chia thành hai lớp, nhưng câu hỏi đặt ra là liệu nó có là cần thiết để chúng tôi thêm tính năng phân đoạn thủ công này. Không, bởi vì svm có một kỹ thuật gọi là thủ thuật hạt nhân, đây là một tính năng thấm sâu vào không gian đầu vào và biến nó thành không gian nhiều chiều hơn, tức là nó không chia vấn đề thành các vấn đề riêng biệt, những tính năng này được gọi là hạt nhân. Tóm lại, nó thực hiện một số chuyển đổi dữ liệu phức tạp và sau đó tìm ra cách phân chia dữ liệu dựa trên các nhãn hoặc đầu ra được xác định trước của chúng tôi.
margin là khoảng cách từ siêu phẳng đến hai điểm dữ liệu gần nhất tương ứng với bộ phân loại. Trong ví dụ về táo và lê do người bán đặt, lề là khoảng cách giữa que và hai quả táo và lê gần nhất. Điều quan trọng ở đây là phương pháp svm luôn cố gắng tối đa hóa lề này, do đó thu được một siêu phẳng có khoảng cách xa nhất từ quả táo và quả lê. Do đó, svm giảm thiểu việc phân loại sai các điểm dữ liệu mới được giới thiệu
Để tìm lời giải của svm, chúng ta trực tiếp sử dụng thư viện sklearn.
Chúng ta sẽ sử dụng hàm ***sklearn.svm.svc*** tại đây. Các bài toán thực tế thường dùng thư viện libsvm viết bằng c, có apis cho python và matlab.
là một kỹ thuật phân loại khá phổ biến và máy vectơ hỗ trợ có nhiều ưu điểm, bao gồm khả năng tính toán hiệu quả trên các tập dữ liệu lớn. Bạn có thể liệt kê thêm lợi ích của phương pháp này, ví dụ:
Nhược điểm:
Kết luận: Support Vector Machines là một phương pháp hiệu quả để giải quyết các vấn đề về phân loại dữ liệu. Nó là một công cụ hiệu quả để giải quyết các vấn đề như xử lý ảnh, phân loại văn bản và phân tích ý kiến. Một trong những điều làm cho svm trở nên hiệu quả là việc sử dụng kernel, làm cho phương thức truyền không gian trở nên linh hoạt hơn.




